Tứ giác nội tiếp là nội dung quan trọng trong chương trình hình học lớp 9. Cùng ôn tập lại khái niệm, tính chất, dấu hiệu nhận biết tứ giác nội tiếp trong bài viết sau để có thể áp dụng giải các bài tập liên quan nhé!
Tứ giác nội tiếp là gì? Định lý về tứ giác nội tiếp
Tứ giác nội tiếp của đường tròn là tứ giác có 4 đỉnh được nằm trên đường tròn đó. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác.
Định lý về tứ giác nội tiếp:
- Định lý thuận: Trong một tứ giác nội tiếp, tổng số đo của hai góc đối diện bằng 180°.
- Định lý đảo: Nếu tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.

Tính chất tứ giác nội tiếp
Ta có 4 tính chất cơ bản của tứ giác nội tiếp sau đây:
- Tính chất 1: Mọi tam giác đều có một đường tròn ngoại tiếp, tuy nhiên không phải mọi tứ giác đều nội tiếp đường tròn.
- Tính chất 2: Tâm đường tròn ngoại tiếp tứ giác nội tiếp là giao điểm của các đường trung trực của các cạnh.
- Tính chất 3: Nếu như tứ giác nội tiếp có 2 góc đối diện là góc vuông thì tâm đường tròn ngoại tiếp sẽ là trung điểm của đường chéo nối liền 2 đỉnh đó.
- Tính chất 4: Nếu như tứ giác nội tiếp có 2 góc vuông cùng nhìn 1 cạnh thì tâm đường tròn ngoại tiếp là trung điểm của cạnh mà cả 2 góc sẽ cùng nhìn vào cạnh đó.

Các em học sinh cần đặc biệt ghi nhớ nội dung này để có thể vận dụng làm bài tập hiệu quả.
Xem thêm: Bán kính, đường kính ký hiệu là gì? Cách tính bán kính, đường kính hình tròn
Các dấu hiệu giúp nhận biết tứ giác nội tiếp
Để nhận biết được tứ giác nội tiếp ta cần dựa vào những dấu hiệu cơ bản sau đây:
- Tứ giác nội tiếp là tứ giác có tổng của 2 góc đối sẽ bằng 180°
- Góc ngoài tại một đỉnh nếu như bằng góc trong của đỉnh đối diện thì đó là tứ giác nội tiếp
- Tứ giác nội tiếp có 4 đỉnh được cách đều một điểm cố định, điểm này là tâm của đường tròn ngoại tiếp tứ giác.
- Tứ giác nội tiếp có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc a
Lưu ý: Trong các hình đã học, các hình như hình vuông, hình chữ nhật, hình thang cân nội tiếp được đường tròn.
Bài tập tứ giác nội tiếp
Dạng 1: Yêu cầu chứng minh tứ giác nội tiếp
Phương pháp giải: Để có thể chứng minh tứ giác nội tiếp ta có thể sử dụng một trong những cách cơ bản sau đây:
- Cách 1. Chứng minh tứ giác đó có tổng 2 góc đối đều bằng 180°
- Cách 2. Chứng minh tứ giác đó có 2 đỉnh kề nhau và cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc a
- Cách 3. Chứng minh tứ giác đó có góc ngoài tại một đỉnh bằng góc trong đỉnh đối diện
- Cách 4. Tìm được một điểm được cách đều bốn đỉnh của tứ giác.

Xem thêm: Cát tuyết là gì? Cách vẽ và giải bài tập về cát tuyến của đường tròn
Bài 1: Ta có tứ giác ABCD nội tiếp (O), trong đó M là điểm chính giữa của cung AB. Thực hiện nối M với D, M với C cắt AB lần lượt tại E và P. Hãy chứng minh rằng PEDC là tứ giác nội tiếp.
Hướng dẫn:
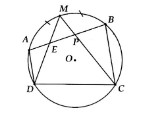
Ta có:
Góc AED = 1/2 (sđ cung AD + sđ cung MB)
= 1/2 sđ cung DM = góc MCD
=> góc DEP + góc PCD = 180°
=> tứ giác PECD nội tiếp
Bài 2: Cho hình thang ABCD (AB//CD, AB < CD) với góc C = góc D = 60°, CD = 2AD. Hãy chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn
Hướng dẫn:
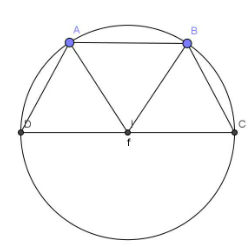
Ta gọi I là trung điểm của CD
Có IC = AB và IC // AB => ICBA là hình bình hành
=> BC = AI (1)
Tương tự, ta có AD = IB (2)
ABCD là hình thang với góc C = góc D = 60° vì thế nên ABCD là hình thang cân (3)
Từ (1), (2) và (3) ta có hai tam giác ICB; IAD đều hay bốn điểm A, B, C, D cùng thuộc một đường tròn.
Dạng 2: Vận dụng tứ giác nội tiếp để chứng minh
Với dạng bài này ta sẽ sử dụng các tính chất của tứ giác nội tiếp nhằm để chứng minh các góc bằng nhau, các đường thẳng song song hoặc đồng quy, các đoạn thẳng bằng nhau, tam giác đồng dạng…
Bài 1: Cho hai đường tròn (O) và (O’) được cắt nhau tại hai điểm A và B. Trong đó đường thẳng OA cắt (O), (O’) lần lượt tại điểm thứ hai C và D, còn đường thẳng O’A cắt (O), (O’) lần lượt tại điểm thứ hai E, F.
- Hãy chứng minh 3 đường thẳng AB, CE và DF đồng quy tại điểm I
- Chứng minh BEIF nội tiếp đường tròn
Hướng dẫn:
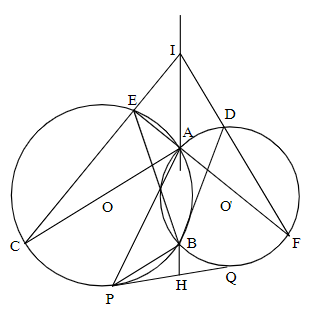
a) Ta có:
– Góc ABC = 90° (góc nội tiếp chắn nửa đường tròn)
– Góc ABF = 90° (góc nội tiếp chắn nửa đường tròn) => B, C, F thẳng hàng.
Vì AB, CE và DF la 3 đường cao của tam giác ACF nên chúng đồng quy.
b) Góc IEF = góc IBM = 90°
=> BEIF là tứ giác nội tiếp đường tròn
Bài viết trên đây chúng ta đã có thể nắm rõ được dấu hiệu nhận biết tứ giác nội tiếp, cũng như tính chất và các dạng bài tập vận dụng để từ đó có thể áp dụng giải bài tập liên quan.



