Trung vị là khái niệm toán học thường dùng trong xác suất, thống kê. Mặc dù khá phổ biến nhưng không phải ai cũng hiểu rõ được khái niệm này. Nội dung sau đây chúng ta sẽ cùng tìm hiểu trung vị là gì, cách tính trung vị và ứng dụng của đại lượng này trong cuộc sống!
Trung vị là gì trong toán học?
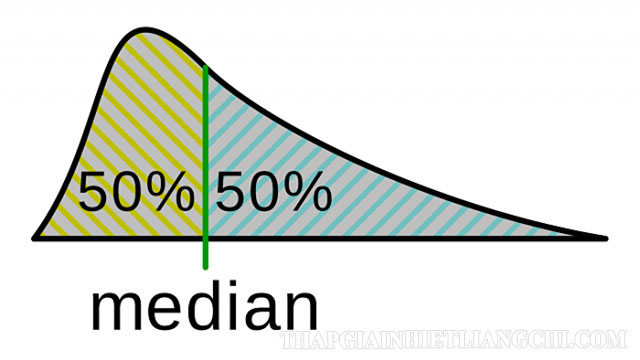
Trung vị có tên tiếng anh là median, đây là giá trị ở giữa trong một tập hợp số. Nếu muốn tính được trung vị chúng ta cần phải sắp xếp các số trong tập hợp đó theo thứ tự tăng hay giảm dần và lấy giá trị ở giữa.

Trường hợp số lượng các số trong tập hợp là số lẻ thì giá trị ở giữa chính là trung vị cho tập hợp số đó. Còn nếu như số lượng các số trong tập hợp là các số chẵn, thì trung vị chính là trung bình cộng của hai giá trị ở giữa.
Đặc điểm của trung vị
Sau khi hiểu được trung vị, nội dung sau đây chúng ta sẽ cùng nhau tìm hiểu các đặc điểm cơ bản của trung vị như sau:
- Nếu muốn xác định trung vị thì chúng ta cần sắp xếp giá trị theo thứ tự từ thấp cho đến cao.
- Với tập hợp dữ liệu có số lượng dữ liệu là số lẻ, ta có trung vị là giá trị đứng ở giữa.
- Tập hợp dữ liệu có số lượng dữ liệu là số chẵn, ta có trung vị là giá trị trung bình của cặp số ở giữa trong tập hợp dữ liệu.
- Trung vị có thể thay thế cho giá trị trung bình trong trường hợp tập hợp dữ liệu có những điểm ngoại lai. Điểm ngoại lai là những giá trị có sự chênh lệch lớn, chúng có thể là quá cao hoặc quá thấp với giá trị khác của tập hợp dữ liệu.
- Tuy nhiên trung vị sẽ không bị ảnh hưởng nhiều bởi những điểm ngoại lai.
Cách tính trung vị
Công thức chung
Ta có công thức để tính trung vị như sau:
{(n + 1) ÷ 2} số thứ tự
Trong đó: “n” là số mục của tập hợp.
Ví dụ: Ta có tập hợp với những số như sau: 1,3,5,7,9, vậy ta có trung vị được tính toán như sau: {(5 + 1) ÷ 2 }= 3.
Trong tập hợp này thì trung vị đứng ở vị trí thứ 3 trong tập hợp giá trị và đó là con số 5.
Đối với tập hợp có số giá trị lẻ
Với tập hợp số với những giá trị là lẻ thì trung vị chính là giá trị được nằm ở giữa của tập hợp.
Ví dụ: Ta có tập hợp số với những giá trị sau 1,3,4,6,7, vậy trung vị chính là số 4, bởi trước số 4 có hai giá trị là 1 và 3 và sau số 4 cũng có hai giá trị là 6 và 7.
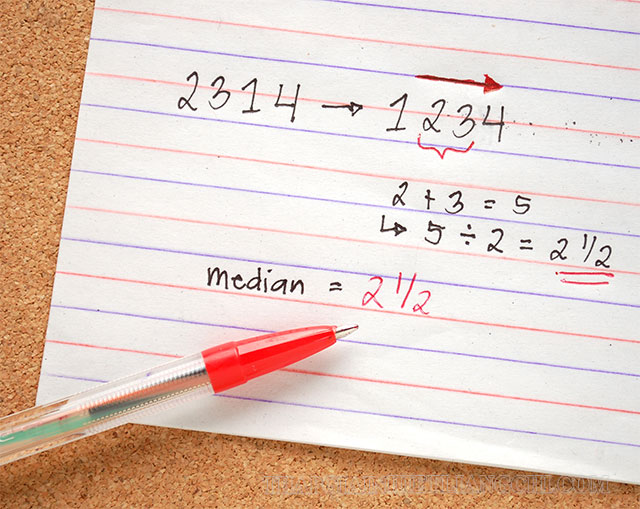
Xem thêm: Tứ phân vị là gì? Ý nghĩa, cách tính tứ phân vị và ví dụ
Với tập hợp số giá trị là chẵn
Tập hợp số có giá trị là chẵn thì trung vị sẽ là giá trị trung bình của cặp số ở giữa của tập hợp.
Ví dụ: Có tập hợp số với những giá trị như 1,2,4,5,8,9, có thể thấy tập hợp này có 6 giá trị, cặp giá trị ở giữa ta có 4 và 5. Để tính được trung vị của dãy số này ta tính như sau: (4+5)/2 = 4,5. Vậy trung vị của dãy số này là 4,5.
Sự khác biệt của số trung bình và trung vị
Số trung bình và trung vị đều là những số nhằm để đại diện cho một tập hợp số, tùy vào từng trường hợp cụ thể mà chúng ta nên dùng số trung vị thay vì số trung bình.
Khi tập hợp số có chứa những giá trị ngoại lệ (outliers), có nghĩa là một số giá trị trong tập hợp rất lớn hay rất nhỏ so với các giá trị khác, thì số trung bình sẽ có thể bị ảnh hưởng nhiều bởi những giá trị này.
Trong khi đó thì trung vị không bị ảnh hưởng bởi những giá trị ngoại lệ này, nhờ đó giúp chúng ta có những đánh giá chính xác về sự phân bố của tập hợp số.
Ví dụ: Cho tập hợp số sau: {1, 2, 3, 4, 5, 100}, ta có số trung bình của tập hợp này là: (1 + 2 + 3 + 4 + 5 + 100) / 6 = 19.17

Như vậy có thể thấy số trung bình của tập hợp số này không phản ánh được chính xác sự phân bố của tập hợp số. Trường hợp này ta nên dùng số trung vị để có được đại diện chính xác hơn đối với tập hợp số:
Trung tâm của tập hợp số được sắp xếp là giá trị ở giữa: {1, 2, 3, 4, 5, 100} Vậy thì ta có thể thấy trong tập hợp này thì số 3 chính là trung vị của tập hợp số.
Xem thêm: Hàm số lượng giác là gì? Phương trình lượng giác cơ bản thường gặp
Ứng dụng của trung vị
Phân tích dữ liệu
Trung vị được ứng dụng trong phân tích dữ liệu nhằm đánh giá sự phân bố của một biến. Thường thì ta sẽ dùng trung vị khi các biến có sự phân bố không đối xứng, có nhiều giá trị ngoại lệ hay những giá trị có khác biệt quá lớn.

Ứng dụng trong xác suất
Ứng dụng của trung vị trong xác suất để nhằm thực hiện các tính toán, khoảng tin cậy, khoảng tin cậy tối thiểu của một phân phối. Ngoài ra trung vị còn được dùng để tính toán các điểm dừng của phân phối.
Ứng dụng trong mô hình học máy
Trung vị là phương pháp vô cùng đơn giản, hiệu quả nhằm để xử lý các giá trị ngoại lệ của mô hình học máy. Khi huấn luyện mô hình học máy thì loại bỏ hay sửa chữa các giá trị ngoại lệ sẽ có thể dẫn đến làm giảm độ chính xác của mô hình.
Nếu sử dụng trung vị để thay thế các giá trị ngoại lệ này sẽ có tác dụng giúp làm giảm thiểu ảnh hưởng của chúng tới kết quả.
Như vậy có thể thấy trung vị là khái niệm đặc biệt quan trọng ở trong thống kê và xác suất. Chúng có tác dụng giúp chúng ta đánh giá một cách chính xác nhất sự phân bố của tập hợp số, từ đó để loại bỏ ảnh hưởng của những giá trị ngoại lệ.
Hy vọng qua bài viết này bạn đọc đã hiểu rõ hơn về khái niệm, ứng dụng cũng như cách tính trung vị. Từ đó để ứng dụng hiệu quả chúng vào những công việc, lĩnh vực cần sử dụng đại lượng này!



