Hàm số lượng giác là một loại hàm số được sử dụng rộng rãi trong toán học, khoa học và kỹ thuật để giải quyết các vấn đề liên quan đến tam giác và các ứng dụng của chúng. Trong bài viết sau đây, chúng ta hãy cùng đi tìm hiểu xem hàm số lượng giác là gì, các phương trình lượng giác cơ bản thường gặp.
Hàm số lượng giác là gì?
Hàm lượng giác là hàm toán học được sử dụng để mô tả mối quan hệ giữa các góc trong tam giác vuông và các tỉ lệ độ dài của các cạnh tương ứng. Hàm số lượng giác thường được dùng khi nghiên cứu tam giác và các hiện tượng có tính chất tuần hoàn.

Các hàm số lượng giác phổ biến nhất là sin, cos và tan. Các hàm số này được xác định bởi các tỉ lệ độ dài của các cạnh trong tam giác vuông. Theo đó:
- Hàm số sin của một góc được định nghĩa là tỉ lệ giữa cạnh đối diện và cạnh huyền của tam giác vuông chứa góc đó.
- Hàm cos của một góc được định nghĩa là tỉ lệ giữa cạnh kề và cạnh huyền của tam giác vuông chứa góc đó.
- Hàm tan của một góc được định nghĩa là tỉ lệ giữa cạnh đối diện và cạnh kề của tam giác vuông chứa góc đó.
Các hàm số lượng giác này có thể được tính toán bằng cách sử dụng các bảng giá trị hoặc bằng cách sử dụng máy tính hoặc máy tính khoa học.
Phương trình lượng giác là gì?
Phương trình lượng giác là các phương trình có chứa các hàm số lượng giác và được sử dụng để giải quyết các vấn đề liên quan đến tam giác và các ứng dụng của chúng.

Một số phương trình lượng giác cơ bản thường gặp trong toán học bao gồm:
- sin(x) = a/c: Đây là phương trình lượng giác để tìm giá trị của một góc x trong tam giác vuông, biết độ dài của cạnh đối diện a và độ dài của cạnh huyền c.
- cos(x) = b/c: Đây là phương trình lượng giác để tìm giá trị của một góc x trong tam giác vuông, biết độ dài của cạnh kề b và độ dài của cạnh huyền c.
- tan(x) = a/b: Đây là phương trình lượng giác để tìm giá trị của một góc x trong tam giác vuông, biết độ dài của cạnh đối diện a và độ dài của cạnh kề b.
Ngoài ra, còn có nhiều phương trình lượng giác phức tạp hơn, được sử dụng để giải quyết các vấn đề phức tạp trong toán học, khoa học và kỹ thuật.
Công thức tính hàm số lượng giác đầy đủ nhất
Bảng giá trị lượng giác của một số cung và góc đặc biệt
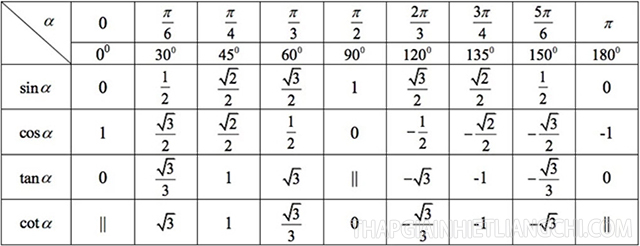
Hệ thức lượng giác cơ bản
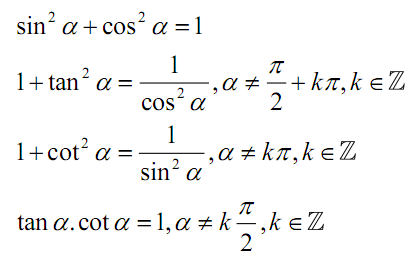
Cung liên kết
Đối với các góc có mối liên kết đặc biệt, điển hình như là bù nhau, đối nhau, phụ nhau, hơn kém pi hoặc hơn kém pi/2, chúng ta có thể áp dụng câu nói sau đây để ghi nhớ dễ dàng hơn: “cos đối, sin bù, tan hơn kém pi, phụ chéo”.

– Hai góc đối nhau:
- cos(–x) = cosx
- sin(–x) = –sinx
- tan(–x) = –tanx
- cot(–x) = –cotx
– Hai góc bù nhau:
- sin (π – x) = sinx
- cos (π – x) = –cosx
- tan (π – x) = –tanx
- cot (π – x) = –cotx
– Hai góc hơn kém π:
- sin (π + x) = –sinx
- cos (π + x) = –cosx
- tan (π + x) = tanx
- cot (π + x) = cotx
– Hai góc hơn và kém π/2:
- sin (π/2 + x) = cos x
- cos (π/2 + x) = -sin x
- tan (π/2 + x) = -cot x
- cot (π/2 + x) = -tan x
– Hai góc phụ nhau:
- sin (π/2 – x) = cos x
- cos (π/2 – x) = sin x
- tan (π/2 – x) = cot x
- cot (π/2 – x) = tan x
Xem thêm: Định lý Ta lét là gì? Những hệ quả của định lý Talet
Công thức nhân

Công thức hạ bậc trong các hàm số lượng giác
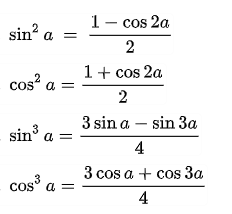
Công thức biến tổng → tích
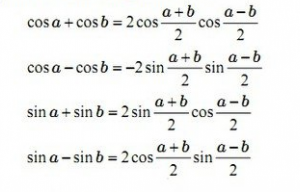
Mẹo giúp dễ dàng ghi nhớ công thức trên hơn: “Cos cộng cos bằng hai cos cos và cos trừ cos bằng trừ hai sin sin; sin cộng sin bằng hai sin cos và sin trừ sin bằng hai cos sin.”
Công thức biến tích → tổng

Xem thêm: Đường trung tuyến là gì? Công thức, tính chất đường trung tuyến của tam giác
Tính nghiệm của các phương trình lượng giác
Tình nghiệm của phương trình lượng giác dạng cơ bản
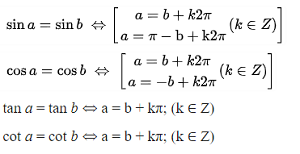
Tính nghiệm của phương trình lượng giác trong các trường hợp đặc biệt:
- sin a = 0 ⇔ a = kπ; (k ∈ Z)
- sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
- sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
- cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
- cos a = 1 ⇔ a = k2π; (k ∈ Z)
- cos a = -1 ⇔ a = π + k2π; (k ∈ Z)
Tóm lại, hàm số lượng giác là một loại hàm số được sử dụng để mô tả mối quan hệ giữa các góc và tỉ lệ độ dài của các cạnh trong tam giác vuông. Các phương trình lượng giác được sử dụng để giải quyết các vấn đề liên quan đến tam giác và các ứng dụng của chúng, và là một phần quan trọng của toán học, khoa học và kỹ thuật.
Trên đây là tất cả các thông tin về hàm số lượng giác là gì, phương trình lượng giác cơ bản thường gặp, mà bạn cần ghi nhớ. Hy vọng, nhữn chia sẻ trên đây sẽ giúp bạn dễ dàng chinh phục được các đề thi sắp tới.



