Hình bình hành là tứ giác với 2 cặp đường thẳng song song và cắt nhau. Nắm vững kiến thức trọng tâm về hình bình hành sẽ giúp các bạn học sinh chinh phục được các dạng bài toán về hình học. Cùng tìm hiểu hình bình hành là gì cũng như dấu hiệu nhận biết hình bình hành trong nội dung dưới đây.
Hình bình hành là gì?
Hình bình hành còn được gọi là hình tứ giác đều có hai cặp cạnh đối song song và bằng nhau. Hình bình hành có 2 đường chéo cắt nhau tại trung điểm mỗi đường chéo, chia hình thành 4 tam giác đồng dạng, chúng là một dạng đặc biệt của hình thang.

Ở trong không gian 3 chiều, khối tương đương với hình bình hành chính là hình khối lục diện.
Ví dụ: Cho hình bình hành ABCD, ta có các cặp như sau: AB//CD và AC// BD.
Tính chất hình bình hành
Hình bình hành sở hữu một số tính chất cơ bản như sau:
- Các cạnh đối diện của hình bình hành là đường đường song song và bằng nhau.
- Các góc đối diện hình bình hành bằng nhau.
- Hình bình hành có 2 đường chéo có cùng độ dài cắt nhau tại trung điểm ở mỗi đường chéo.
- Hai trục của hình bình hành đối xứng với nhau là đường chéo lớn và đường chéo nhỏ.
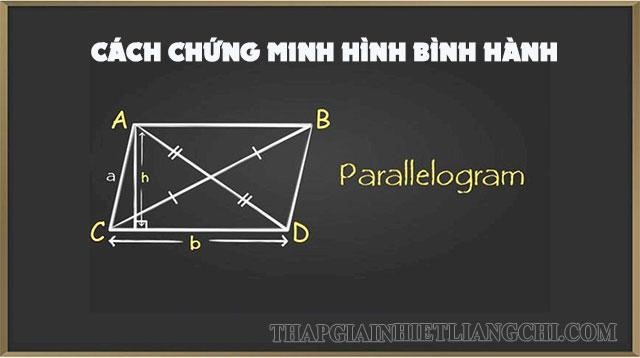
- Diện tích hình bình hành bằng với tích của độ dài cạnh và độ dài đường cao tương ứng với cạnh đó.
- Hình bình hành có chu vi bằng tổng độ dài bốn cạnh của nó.

- Hình bình hành là dạng đa diện lồi (convex polygon).
- Hình bình hành có thể được trở thành hình vuông nếu đường chéo của nó là đường kính của hình vuông đó.
Các tính chất này được áp dụng để nhằm thực hiện giải quyết các bài toán liên quan đến hình bình hành.
Xem thêm: Hình lập phương là gì? Công thức tính diện tích và thể tích hình lập phương
5 dấu hiệu nhận biết hình bình hành
Để nhận biết được hình bình hành chúng ta dựa vào 5 dấu hiệu cơ bản hư sau:
- Dấu hiệu 1: Tứ giác có các cạnh đối song song với nhau là hình bình hành.
Tứ giác ABCD có AB//CD và AD//CB => ABCD là hình bình hành.
- Dấu hiệu 2: Tứ giác có các cạnh đối bằng nhau sẽ là hình bình hành.
Tứ giác ABCD có AB = CD, AD =BC => ABCD là hình bình hành.
- Dấu hiệu 3: Tứ giác có hai cạnh đối song song, bằng nhau chính là hình bình hành.
Tứ giác ABCD có AB//CD và AB = CD hoặc AD//BC và AD = BC => ABCD là hình bình hành.
- Dấu hiệu 4: Tứ giác có các góc đối bằng nhau chính là hình bình hành.

- Dấu hiệu 5: Tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường sẽ là hình bình hành.
Tứ giác ABCD có cạnh AC cắt cạnh BD tại điểm O. Nếu OA = OC, OB = OD => ABCD là hình bình hành.
Xem thêm: Hình thoi là gì? Tính chất và công thức tính chu vi, diện tích hình thoi
Cách chứng minh hình bình hành
Để chứng minh một hình thang là một hình bình hành, chúng ta cần phải chứng minh rằng chúng đáp ứng được những tính chất sau:
- Tính chất 1: Có các cạnh đối diện bằng nhau, song song với nhau.
- Tính chất 2: Sở hữu các góc đối diện bằng nhau.
- Tính chất 3: Có 2 đường chéo cắt nhau tại trung điểm của mỗi đường chéo.
- Tình chất 4: Các đường chéo sở hữu độ dài bằng nhau.
Để chứng minh tính chất 1 và 2, ta có thể áp dụng các định lí hình học hoặc phương pháp đối ngẫu.
Để chứng minh tính chất 3, ta có dùng định lí về đường trung trực. Với một hình thang ABCD, chúng ta cần vẽ đường chéo AC và BD. Vì ABCD là một hình thang, vì thế nên đường trung trực của AB cắt đường trung trực của CD tại điểm E. Đường trung trực của BC cắt đường trung trực AD tại một điểm F.
Vì AE = EC và BF = FD => điểm G là trung điểm của CE, điểm H là trung điểm của DF. Suy ra AG và DH là hai đường chéo của hình thang ABCD được cắt nhau tại trung điểm I của mỗi đường chéo.
Để chứng minh tính chất 4, ta cũng có thể dùng các định lí hình học.
Ví dụ, dùng định lý tam giác đều, bởi vì khi chia hình thang ABCD thành hai tam giác bằng nhau bằng đường chéo AC ta sẽ được 2 tam giác đều AEC và BFD. Vì thế, CE = DF, và AG và DH là đường trung trực của CE và DF tương ứng => AG = DH. Vậy 2 đường chéo của hình thang ABCD có độ dài bằng nhau.
Nếu như một hình thang thỏa mãn các tính chất trên thì nó là hình bình hành.
Công thức tính chu vi và diện tích của một hình bình hành
Công thức tính diện tích
Diện tích hình bình hành được đo bằng độ lớn của bề mặt hình, đó là phần mặt phẳng mà chúng ta có thể nhìn thấy được.
Theo đó, diện tích của hình bình hành được tính theo công thức bằng tích của cạnh đáy nhân với chiều cao: SABCD = a.h
Trong đó:
- S: là diện tích hình bình hành
- a: là cạnh đáy hình bình hành
- h: là chiều cao.

Công thức tính chu vi
Chu vi hình bình hành là tổng độ dài của 4 cạnh với công thức như sau:
C = 2 x (a+b)
Trong đó:
- C là chu vi hình bình hành.
- a và b là cặp cạnh kề nhau.
Tính chất đường chéo của một hình bình hành
Đường chéo hình bình hành là đoạn thẳng được dùng để nối hai đỉnh không kề nhau của hình. Hình bình hành có hai đường chéo là đường chéo lớn và đường chéo nhỏ. Đường chéo hình bình hành sở hữu những tính chất sau:
- Độ dài 2 đường chéo như nhau.
- Đường chéo chia hình bình hành thành 2 tam giác đều, đồng dạng với nhau.
- Độ dài đường chéo lớn bằng tích căn bậc hai tổng bình phương của độ dài 2 cạnh kề hình bình hành.
- Độ dài đường chéo nhỏ bằng tích căn bậc hai tổng bình phương độ dài 2 đường cao tương ứng với 2 cạnh kề hình bình hành.
Những tính chất này đặc biệt hữu ích trong việc giải các bài toán liên quan đến hình bình hành, cũng như đường chéo của nó.
Bài tập vận dụng
Bài 1: Cho hình bình hành ABCD với cạnh AB=CD=5cm, cạnh AC=BD=12cm. Yêu cầu tính chu vi của hình bình hành ABCD?
Hướng dẫn:
Chu vi hình bình hành ABCD là:
C=2.(a+b)=2.5.12= 120 cm.
Bài 2: Cho hình bình hành MNPQ, tại điểm M kẻ đường thẳng MH sao cho AH vuông góc PQ. Biết rằng MH=8cm, PQ=15cm. Hãy tính diện tích của hình bình hành MNPQ?
Hướng dẫn:
Ta có diện tích của hình bình hành MNPQ như sau:
S=a.h=MH.PQ= 8.15= 120 cm2.
Bài 3: Một hình bình hành ABCD với cạnh đáy AB = 15cm, chiều cao AH bằng 3/5 cạnh đáy. Bạn hãy tính diện tích của hình bình hành này.
Hướng dẫn:
Chiều cao hình bình hành ABCD bằng: 15 x 3/5 = 9 cm
=> Diện tích của hình bình hành ABCD bằng: 15 x 9 = 135 cm2

Bài 4: Cho hình bình hành ABCD, gọi E là trung điểm của AB, còn F là trung điểm của CD. Hãy chứng minh: DE = BF
Hướng dẫn:
Theo tính chất của hình bình hành AB = CD
EB = 1/2 AB (giả thuyết)
FD = 1/2 CD (giả thuyết)
=> EB = FD (1)
Mà AB // CD (giả thuyết)
=> BE // FD (2)
Từ (1) và (2) ta có tứ giác BEDF là hình bình hành vì có một cặp cạnh đối song song và bằng nhau.
=> DE = BF (dựa theo tính chất hình bình hành)
Bài 5: Cho hình bình hành ABCD, gọi H và K lần lượt là chân đường vuông góc kẻ từ A và từ C cho đến BD.
a) Hãy chứng minh AHCK là hình bình hành
b) Gọi M là giao điểm của AK và BC, còn N là giao điểm của CH và AD. Hãy chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Hãy chứng minh rằng O, M, N thẳng hàng
Hướng dẫn:
a) Xét AHD và CKB có: H = K = 90⁰
AD = BC
D1 = B1 (so le trong)
=> AHD = CKB
=> AH = CK
Ta lại có AH // CK (cùng vuông góc với BD)
=> Vậy nên AHCK là hình bình hành.
b) Tứ giác AHCK là hình bình hành, vì thế ta có AK // CH hay AM // CN.
Ngoài ra, AN // CM (ABCD là hình bình hành)
=> Vì ANCM là hình bình hành nên suy ra AN = CM.
c) Hình bình hành AHCK có O là trung điểm HK, vì thế nên O là trung điểm của AC (tính chất đường chéo hình bình hành).
Hình bình hành ANCM có O là trung điểm của AC => O là trung điểm của MN.
=> M, N, O thẳng hàng.
Việc nắm rõ dấu hiệu nhận biết hình bình hành, cũng như các kiến thức về hình bình hành là rất cần thiết để áp dụng chúng nhằm thực hiện giải các bài tập liên quan.



