Dao động điều hòa là nội dung kiến thức đặc biệt quan trọng đối với chương trình Vật lý. Vậy cùng tìm hiểu dao động điều hoà là gì, cũng như bài tập, công thức về dao động điều hòa như thế nào ngay trong bài viết sau đây!
Khái niệm và phương trình dao động điều hoà
Khái niệm dao động điều hoà là gì?
Dao động điều hoà là dao động tuần hoàn mà phương trình trạng thái được biểu diễn ở dưới dạng các hàm điều hoà (hàm sin hoặc cosin). Thời gian để giúp vật thực hiện một dao động toàn phần là một chu kỳ T.
Số dao động toàn phần mà vật thực hiện được trong thời gian 1s là tần số f.

Theo đó, ta có công thức dao động điều hoà thức sau: T=1/f
Ở công thức này, dao động cơ được chuyển động qua lại quanh một vị trí cân bằng. Ví dụ về dao động điều hoà như: Sự chuyển động đung đưa của chiếc lá, chuyển động của con lắc đồng hồ,…
Phương trình dao động điều hoà
Khi một điểm bất kỳ P được dao động điều hoà trên một đoạn thẳng từ P1 đến P2, ta có thể coi điểm P này là hình chiếu của một điểm M tương ứng được chuyển động tròn đều với tốc độ góc ω, trên đường tròn với đường kính là đoạn thẳng P2P1.
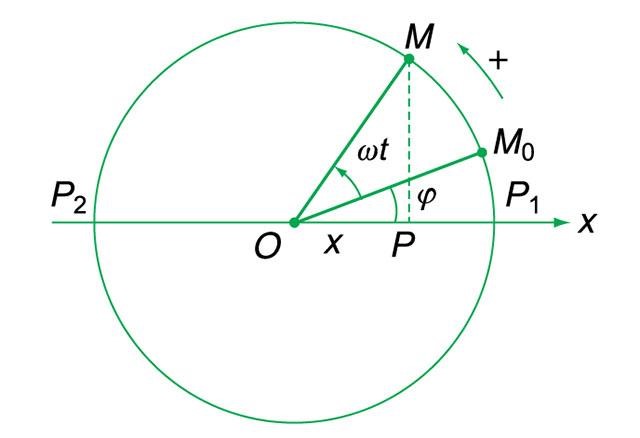
Giả sử t = 0, vật ở vị trí M0 sẽ được xác định bằng góc φ.
Tại thời điểm t, M có vị trí là (ωt + φ).
Lúc này, hình chiều P của M có tọa độ x = A cos(ωt + φ).
Vậy ta có phương trình của dao động điều hoà là: x = A cos(ωt + φ)
Trong đó:
- A: Là biên độ giao động (A>0)
- ω: Là tốc độ góc trong chuyển động tròn đều hoặc tần số góc ở trong dao động điều hoà
- ωt + φ: Là pha của dao động tại thời điểm t
- φ: Pha ban đầu của giao động, đơn vị là rad (-π≤φ≤π)
Xem thêm: Dao động tắt dần là gì? Nguyên nhân, ứng dụng, công thức tính
Các đại lượng đặc trưng của dao động điều hòa
Trong dao động điều hoà, chúng ta cần phải nắm vững được các đại lượng đặc trưng bao gồm: chu kỳ, vận tốc, tần số dao động, tần số góc, gia tốc dao động điều hoà.
Chu kì, tần số và tần số góc trong dao động điều hoà
Chu kỳ chính là khoảng thời gian để vật thực hiện được một giao động toàn phần. Đơn vị của chu kỳ là: giây (s)
Còn tần số f của dao động điều hoà là số dao động toàn phần được thực hiện được ở trong một giây. Đơn vị của tần số là: héc (Hz)
Tần số góc ω là đại lượng được liên hệ với chu kì T hay với tần số f bởi hệ thức sau đây: ω=T2π=2πf
Tần số góc có đơn vị là rad/s.
Một chu kì dao động vật sẽ đi được với một quãng đường là S = 4A.
Vật có chiều dài quỹ đạo chuyển động là L = 2A.

Vận tốc ở trong dao động điều hoà
Công thức của vận tốc của dao động điều hoà như sau:
v=x′=−Aωsin(ωt+φ)=ωAcos(ωt+φ+2π)
Tại vị trí cân bằng, vận tốc có độ lớn cực đại là: vmax=ωA
Vận tốc nhanh pha hơn li độ một góc và vận tốc được đổi chiều tại biên độ.
Xem thêm: Sóng cơ là gì? Phân loại, các đặc trưng của sóng cơ
Đại lượng gia tốc trong dao động điều hoà
a=v′=x′′=−ω2A=−ω2Acos(ωt+φ)=ω2Acos(ωt+φ+π)
– Vecto của gia tốc luôn hướng về vị trí cân bằng
– Độ lớn của gia tốc được tỉ lệ với độ lớn của li độ
– Ở vị trí biên gia tốc đạt được độ lớn cực đại
– Ở vị trí cân bằng, độ lớn của gia tốc bằng 0
– Gia tốc nhanh pha hơn độ lớn một góc và cũng ngược pha với số độ góc.
Các dạng bài tập dao động điều hoà thường gặp
Dạng 1: Bài tập xác định đại lượng đặc trưng trong dao động điều hoà
Đây là dạng bài toán xác định đại lượng như biên độ A, vận tốc góc ω, chu kỳ, tần số, pha ban đầu từ số dữ kiện cho trước,… bằng việc đồng nhất với phương trình dao động điều hoà chuẩn.
Dạng 2: Tìm kiếm quãng đường mà vật đi được
Dạng 1: Yêu cầu xác định quãng đường vật đi được ở trong một khoảng thời gian Δt:
– Trong khoảng thời gian t = 1T vật đi được quãng đường S = 4A
– Trong thời gian nửa chu kỳ T, vật đi được một quãng đường S = 2A
Bước 1: Xác định vị trí hay thời điểm t1, t2 cho trước ở trên đường tròn. Tìm Δt, Δt = t2 – t1.
Bước 2: Tách Δt = n.T + t* ⇔ Δφ = n.vong + φ*
Bước 3: Tìm quãng đường. S = n.4.A + S*.
Căn cứ vào vị trí, chiều chuyển động của vật tại t1 và t2 để có thể tìm ra được S3.
Dạng 2: Bài toán yêu cầu xác định Smax – Smin vật đi được trong khoảng thời gian Δt (Δt < T/2):
– Quãng đường max đối xứng qua vị trí cân bằng
– Quãng đường min đối xứng qua biên.

Ví dụ: Ta có phương trình dao động điều hoà x = 6cos(4πt + π/3) cm. Yêu cầu thực hiện tính quãng đường vật đi được sau 1s kể từ thời điểm ban đầu.
- 24 cm
- 60 cm
- 48 cm
- 64 cm
Hướng dẫn:
Ta có:
T = 2π/ ω = 0,5s ⇒ Δt/T = 1/0,5 = 2
⇒ Δt = 2T
⇒ S = 2. 4A = 48cm
Vậy đáp án đúng là C.
Dạng 3: Tính tốc độ trung bình, vận tốc trung bình
Tổng quát: v = S/t
Trong đó:
- S: là quãng đường mà vật đi được trong khoảng thời gian t
- t: là thời gian vật đi được trong quãng đường S
Bài toán yêu cầu tính tốc độ trung bình cực đại của vật ở trong khoảng thời gian t: vmax = Smax/t
Bài toán về tính tốc độ trung bình nhỏ nhất của vật trong khoảng thời gian t: vmin = Smin/t
Vận tốc trung bình: vtb = Δx/t
Trong đó:
- Δx: Là độ biến thiên về độ dời của vật
- t: là thời gian để vật thực hiện được độ dời Δx.
Xem thêm: Mạch dao động là gì? Nguyên lý, đặc điểm, công thức mạch dao động
Một số bài tập cơ bản về dao động điều hoà
Bài tập 1: Cho một vật dao động điều hoà có phương trình x = 5cos(4πt + π). Yêu cầu hãy xác định chu kì, biên độ và vị trí tại thời điểm t = 0?
Hướng dẫn:
Dựa vào phương trình dao động điều hoà, ta có:
A = 5, T = 2π/ω = 2π/4π = 1/2
Ở thời điểm t = 0, khi thay thế vào phương trình ta được: x = 5cos(π) = -5
Bài tập 2: Một vật dao động điều hoà theo phương trình x = 2cos(2πt + π/4) cm. Vậy tốc độ trung bình của vật trong khoảng thời gian từ t = 2s đến t = 4,875s sẽ là:
- 7,45m/s
- 8,14cm/s
- 7,16cm/s
- 7,86cm/s
Hướng dẫn:
Quãng đường S trong khoảng thời gian Δt = t2 – t1 = 2,875s
Tốc độ trung bình: v = S/ Δt = 8,14 cm/s
Vậy đáp án đúng là B.

Bài tập 3: Vận tốc của một hạt dao động điều hoà ở vị trí cân bằng là:
- 0.
- v min.
- v max.
- v^2.
Đáp án đúng là: B
Bài tập 4: Vận tốc của một hạt (v) dao động điều hoà ở một thời điểm bất kỳ được cho bởi:
- ω √r^2 – x^2.
- ω √x^2 – r^2.
- ω^2 √r^2 – x^2.
- ω^2 √x^2 – r^2.
Đáp án đúng là A
Bài tập 5: Con lắc đơn có tần số dao động là:
- 1 / 2π √L / g.
- 1 / 2π √g / L.
- 2π √L / g.
- 2π√g / L.
Đáp án đúng là: B.
Như vậy, thông qua bài viết này chúng ta đã có thể hiểu được dao động điều hoà là gì, cũng như công thức tính và bài tập áp dụng cụ thể về dao động điều hoà. Hy vọng, những thông tin này sẽ thực sự hữu ích, giúp các bạn học sinh có thể làm tốt các bài tập liên quan đến dao động điều hoà.



